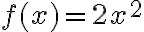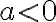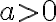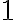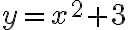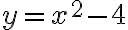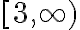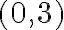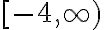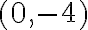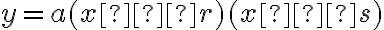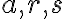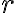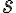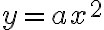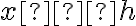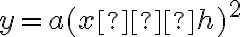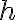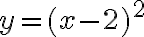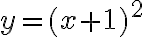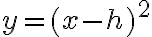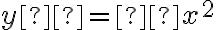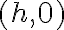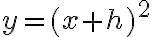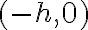Topic outline
-
-
In this subtopic, you will learn about graphing quadratic functions. The graph of a quadratic is a parabola, which may open upwards or downwards. The vertex or turning point of the parabola is an important feature, as are the
 -intercepts (if it has any) and the
-intercepts (if it has any) and the 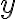 -intercept (there will always be one).
-intercept (there will always be one). Our resident engineer, Dr Kim Blackmore, explains why knowing about quadratic functions is important for engineers:
"Quadratic functions have always been a personal favourite of mine - they have a nice parabola shape and are symmetrical, which appeals to me! In engineering, we use quadratic functions to optimise performance. We examine the various inputs and output measurements and then try to determine at what point the maximum efficiency occurs - which will be the turning point of the quadratic function. For example, in chemical engineering, quadratic functions can be used to find the optimal amount of a fuel additive to use to improve the performance of a vehicle."
Quadratic Functions
We have met quadratic expressions several times already in this course.
(Note that .)We will now concentrate on understanding and graphing quadratic functions that can be expressed as:
.)We will now concentrate on understanding and graphing quadratic functions that can be expressed as:or
Quadratic functions can be used to describe situations where the speed or rate of change of an object changes as it moves. The motion of projectiles (rockets, balls, paper planes) are good examples of situations that can be modelled with quadratic functions. To sketch a graph of a quadratic function we find the important features, namely the
 -intercepts (if any), the
-intercepts (if any), the  -intercept, and the vertex. From these, we can sketch the
function, and find the equation in vertex form:
-intercept, and the vertex. From these, we can sketch the
function, and find the equation in vertex form: 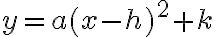 .
.
A quadratic function in one variable, sayThe ‘standard form’ of a quadratic
 , can be written in the form
, can be written in the form 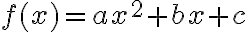 where
where 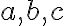 are real numbers and
are real numbers and 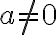 . This is called the standard
form. We can label the output
. This is called the standard
form. We can label the output 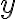 , so quadratic functions can also be expressed as
, so quadratic functions can also be expressed as 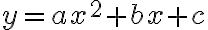 .
We will examine the effect of each of the parameters,
.
We will examine the effect of each of the parameters, 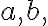 and
and 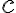 .
.
We will start by setting parameters
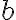 and
and 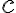 to zero and examining the effect of
to zero and examining the effect of 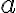 .
.The shape of each curve is a parabola. Each has a turning point or vertex. If the graph opens up, it is called concave up and the vertex is a minimum. If the graph opens down, it is called concave down and the vertex is a maximum.
 Activity 6G - Factored Form
Activity 6G - Factored FormWhat
Complete the question to check your knowledge of factored form.How
- Enter the response to the question in the space provided.
 Activity 6H - Factored Form
Activity 6H - Factored FormWhat
This activity contains questions which can be used to self-check your understanding of factored form.How
- Select the correct response to each of the multiple-choice questions.
Applying all three transformations we have examined so far, we obtain a very useful form of the general quadratic:Vertex Form of a Quadratic
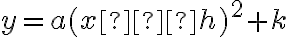 .
.
Consider the case when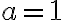 . The smallest value of
. The smallest value of 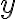 is
is 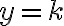 which occurs when
which occurs when 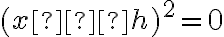 . We solve this to find that the minimum value occurs when
. We solve this to find that the minimum value occurs when 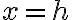 and
and 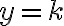 . This is the coordinate
. This is the coordinate 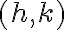 .
.
The vertex form gets its name because we can immediately read the vertex from the quadratic: the vertex occurs at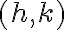 . We use
. We use 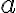 to tell us whether the vertex is a
maximum or a minimum.
to tell us whether the vertex is a
maximum or a minimum.  Activity 6J - Vertex Form
Activity 6J - Vertex FormWhat
This activity contains questions to check your knowledge of vertex form.How
- Select the correct response to each of the multiple-choice questions.
To graph a quadratic function we should:Graphing Quadratic Functions
- Find the x-intercepts (if any).
- Find the y-intercept.
- Find the vertex.
- Determine if the quadratic opens up or down and determine if the vertex is a maximum or a minimum.
- Plot the intercepts and the vertex. Connect these points with a smooth curve.
 Activity 6K - Graphing a Quadratic Function
Activity 6K - Graphing a Quadratic FunctionWhat
Use this activity to check your understanding of graphing quadratic equations.How
- Manipulate the sliders to graph
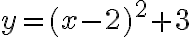 .
. - Click the share icon (
 ) in the graphing tool and export an image of your completed graph.
) in the graphing tool and export an image of your completed graph. - Annotate your graph to show all of the important features.
- Share your completed graph in the Padlet below by opening the Padlet link below and clicking the plus sign at the bottom right-hand side of the screen, then uploading the image of your finished graph.
- Manipulate the sliders to graph
-
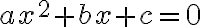
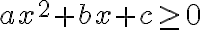
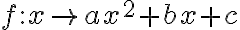
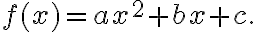
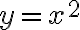
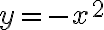
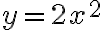
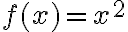
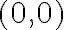
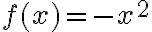
![(-\infty, 0] (-\infty, 0]](https://uo.unisa.edu.au/filter/tex/pix.php/8bb8e3006289394bd593c5b7a4904dd6.gif)