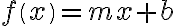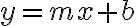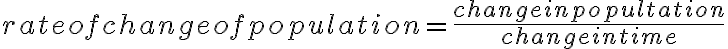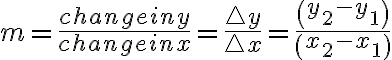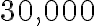Topic outline
-
-
This section will provide you with an opportunity to draw a sketch of the equation of the line in order to understand the effect of change in the value of the slope of a line and its vertical intercept.
Linear Functions and Forms of Lines: Part B (21m 24s)Watch
Linear Functions
Linear functions describe quantities that have a constant rate of increase (or decrease). A linear function is a function that can be written:
for real-valued constants
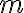 and
and 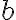 . We call the constants
. We call the constants 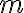 and
and 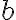 parameters for the family of linear functions.
parameters for the family of linear functions.We can also call the output of the function
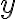 , in which case we describe our family of linear functions as:
, in which case we describe our family of linear functions as:Recall: We solved linear equations in a previous week. Now we are investigating the properties of the whole family of linear functions. Being able to solve linear equations is a useful skill in exploring linear functions.
 Activity 4M - Linear Functions
Activity 4M - Linear FunctionsWhat
This activity lets you practice applying your knowledge of linear functions.How
- Enter the correct responses to each question in the space provided.
Now, complete the graph below to show the population as indicated by the linear equation
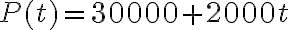 . Note, you do not have to share this graph, however, you should save a copy as we will be using it in the subsequent activities.
. Note, you do not have to share this graph, however, you should save a copy as we will be using it in the subsequent activities. - Based on the graph in Activity 4M, we observe several features in linear functions:
- The graph is a straight line
- The rate of change is constant
These are properties of all linear functions and give rise to several important features of this family of functions.
Gradient
We observed in Activity 4M that a unit increase in
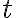 corresponds to an increase of
corresponds to an increase of 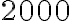 in
in 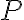 . That is, each year the population increases by
. That is, each year the population increases by 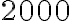 . Because the rate of change of a linear function is constant, we can use any two points to find the rate of change.
. Because the rate of change of a linear function is constant, we can use any two points to find the rate of change.For this example, the rate of change of population is given as follows:
In general, the rate of change, also called gradient or slope, is the change in
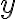 per unit change in
per unit change in  . Given any two points
. Given any two points 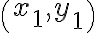 and
and 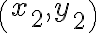 , the gradient
, the gradient 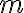 is found by using:
is found by using:This can be seen diagramatically below:

We say that changes in the value of
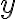 are proportional to changes in the value of
are proportional to changes in the value of  . The valye
. The valye 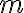 is sometimes called the constant of proportionality.
is sometimes called the constant of proportionality.  Activity 4N - Gradient
Activity 4N - GradientWhat
Use this activity to self-check you knowledge of gradient.How
- To complete this activity, you will need your completed graph from Activity 4M.
- Answer the question below.
 Activity 4O - Gradient as a Rate of Change
Activity 4O - Gradient as a Rate of ChangeWhat
Use these activities to self-check your knowledge of gradient as a rate of change.How
- This activity has two parts. In part A you need to match the functions with their correct graph (you may wish to use a table of values to assist). In part B, drag and drop the text to complete the statements about slope.
Part A:
Part B:
 Activity 4P - Vertical Intercept
Activity 4P - Vertical InterceptWhat
This activity gives you the opportunity to check your knowledge of the vertical intercept as it relates to linear functions.How
- This activity has two parts. In part A you need to match the functions with their correct graph (you may wish to use a table of values to assist). In part B, select the correct answer to the questions about slope.
Part A:
-