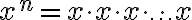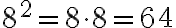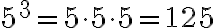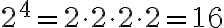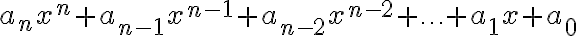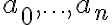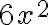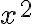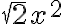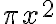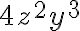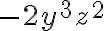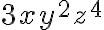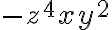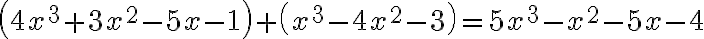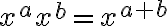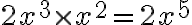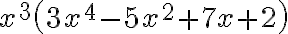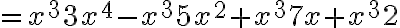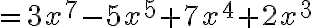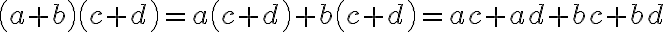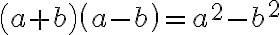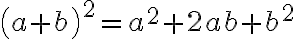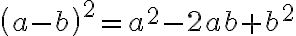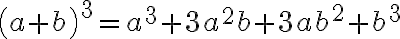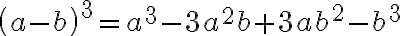Polynomials (10m 23s)Watch
Polynomials: Addition and Subtraction (2m 28s)
Algebraic Expressions
Algebra uses letters such as
and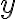 
, to represent numbers. If a letter is used to represent various numbers, it is called a variable. If the letter takes a fixed value, it is called a constant.Many algebraic expressions involve exponents. We will talk about these in greater detail later, but to remind ourselves: natural number exponents are defined as follows:
where we multiply
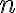copies of on the right side.For example:
Polynomials
A polynomial is an expression that can be written as a term or sum of more than one term. Each term in the polynomial is the product of constants and variables. Since the same variable can be used more than once in such a product, a positive integer exponent of a variable can appear in a term. A polynomial of one term is called a monomial. A polynomial of two terms is called a binomial. A polynomial of three terms is called a trinomial (then we stop labelling them!).
It is customary to write the terms in order of descending powers of the variable. This is called the standard form of a polynomial.
The definition of a polynomial in one variable is:
where
are real numbers, and is a nonnegative integer.
Activity 1G - PolynomialsWhat
This activity will allow you to check your understanding of polynomials.How
- Respond to each of the multiple-choice questions below, identifying each of the following expressions as a monomial, binomial, trinomial or a general polynomial.
Degree of a Polynomial
The degree of a term is the exponent of the variable, or if more than one variable is present, the sum of the exponents of the variables. The degree of a polynomial is the largest of the degrees of the individual terms.
Aside: The degree of a nonzero constant is
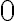. The constant 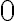has no defined degree (because it can be expressed in many ways: 
).
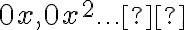Activity 1H - Polynomial DegreesWhat
This activity allows you to check your knowledge of polynomial degrees.How
- Identify the degree of each of the following polynomials.
Like and Unlike Terms
Two or more terms are called like terms if:
- they are both constants, or
- they contain the same variables raised to the same exponents
and differ only, if at all, in their constant coefficients. Terms that are not like terms are called unlike terms.
These are all examples of like terms:
and 
and 
and 
and 
Adding (and Subtracting) Polynomials
The sum of two or more polynomials is found by combining like terms.
For example,
Multiplying Two Monomials
The product of two (or more) monomials is found by using the properties of exponents:
For example:
Activity 1I - Adding, Subtracting and Multiplying MonomialsWhat
This activity will let you practise adding, subtracting and multiplying monomials.How
- Select the correct answer for the multiple responses provided.
Multiplying a Monomial and a Polynomial
The product of a monomial and polynomial is found by using the distributive property. Applying the distributive property in this way is often called expanding.
For example,
Activity 1J - Multiplying a Monomial and a PolynomialWhat
Complete the questions below to check your understanding of how to multiply a monomial and a polynomial.How
- Select the correct multiple-choice responses in the quiz below.
Multiplying Two Binomials
We frequently need to multiply two binomials together. We do this by distributing each term in the first binomial through the second binomial.
This is often called the FOIL method because we multiply together the two First terms. the two Outer terms, the two Inner terms, and the two Last terms
Misconception Alert! The order in which we expand expressions using the distributive law is unimportant. FOIL could also be called LIFO or OLIF or any other arrangement of these letters.
To multiply two polynomials together, we simply generalise the distributive property.
Activity 1K - Multiplying Two BinomialsWhat
This activity allows you to practice multiplying binomials and polynomials.How
- Select the correct response to the multiple-choice questions below.
Special Products
There are some products that occur so frequently that they are called special products. It is helpful to be able to recognise them, but if you can't remember them, you can always work them out using the distributive property.
Difference of two squares:
Square of a sum:
Square of a difference:
Cube of a sum:
Cube of a difference:
Topic outline
-
-
In this section, you will be introduced to algebraic expressions. You will study the degree of terms in such expressions, and like and unlike terms. You will learn basic operations on algebraic expressions such as their addition, subtraction and multiplication. You will learn the rule of expanding a polynomial. In particular, you will explore special products including binomial multiplication using FOIL.
Our resident engineer, Dr Kim Blackmore, explains why knowing about polynomials is important for engineers:
"Polynomial expressions show how numbers combine to describe different relationships in engineering. By using variables and exponents we can represent engineering quantities mathematically and understand how things change in relation to each other, rather than individual numbers. By understanding these sorts of relationships we can ensure that a bridge won't fall down when the wind blows or an earthquake occurs".
-